Answer the following Questions.

1. Choose the correct answer. A thermodynamic state function is a quantity

(i) used to determine heat changes 

(ii) whose value is independent of path 

(iii) used to determine pressure volume work 

(iv) whose value depends on temperature only

Solution :

A thermodynamic state function is a quantity Whose value is independent of a path. Functions like p, V, T etc. depend only on the state of a system and not on the path. 

Hence, alternative (ii) is correct. 

2. For the process to occur under adiabatic conditions, the correct condition is:

(i) ∆T = 0 

(ii) ∆p = 0 

(iii) q = 0 

(iv) w = 0

Solution : A system is said to be under adiabatic conditions if there is no exchange Of heat between the system and its surroundings. Hence, under adiabatic conditions, q = 0. 

Therefore, alternative (iii) is correct,

3. The enthalpies of all elements in their standard states are:

(i) unity 

(ii) zero 

(iii) < 0 

(iv) different for each element

Solution : The enthalpy of all elements in their standard state is zero. Therefore, alternative (ii) is correct 

4. ΔU^⊖ of combustion of methane is −X kJ mol⁻¹. The value of ΔH⊖ is

(i)=ΔU^⊖

(ii) >ΔU^⊖

(iii) <=ΔU^⊖

(iv) = 0

Solution :

SinceΔH^θ=ΔU^θ+Δn_gRT and ΔU^θ=−Xkmol⁻¹

ΔH^θ=(−X)+Δn_gRT

⇒△H^θ<ΔU^θ

Therefore, alternative (iii) is correct. 

5. The enthalpy of combustion of methane, graphite and dihydrogen at 298 K are, –890.3kJmol⁻¹−393.5kJmol⁻¹, and −285.8kJmol⁻¹

 respectively. Enthalpy of formation of CH₄  will be

(i)−74.8kJmol⁻¹

(ii)−52.27kJmol⁻¹

(iii)+74.8kJmol⁻¹

(iv)+52.26kJmol⁻¹

Solution :

According to the question, 

(i)CH₄(g)+2O₂(g)⟶CO₂(z)+2H₂O(g)ΔH=−890.3kJmol⁻¹

(ii)C(x)+O₂(y)⟶CO₂(g)ΔH=−393.5kJmol⁻¹

(iii)2H₂(g)+O₂(z)⟶2H₂O(g)

ΔH=−285.8kJmol⁻¹

Thus, the desired equation is the one that represents the formation of CH₄(g) i.e..,

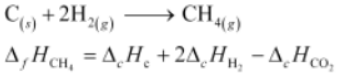
= [-395.5 + 2(-285.8) – (-890.3)] kJ Mol^-1

= -74.8 kJ Mol^-1

∴ Enthalpy of formation of CH₄(g)=−74.8kJmol⁻¹ Hence, alternative (i) is correct.

6. A reaction, A + B → C + D + q is found to have a positive entropy change. The reaction will be
(i) possible at high temperature
(ii) possible only at low temperature
(iii) not possible at any temperature
(iv) possible at any temperature

Solution :
For a reaction to be spontaneous, ΔG should be negative.
ΔG = ΔH – TΔS
According to the question, for the given reaction,
ΔS = positive
ΔH = negative (since heat is evolved)
⇒ ΔG = negative
Therefore, the reaction is spontaneous at any temperature.
Hence, alternative (iv) is correct.

7. In a process, 701 J of heat is absorbed by a system and 394 J of work is done by the system. What is the change in internal energy for the process?

Solution :

According to the first law of thermodynamics,
ΔU = q + W    (i)
Where,
ΔU = change in internal energy for a process
q = heat
W = work
Given,
q = + 701 J (Since heat is absorbed)
W = –394 J (Since work is done by the system)
Substituting the values in expression (i), we get
ΔU = 701 J + (–394 J)
ΔU = 307 J
Hence, the change in internal energy for the given process is 307 J.

8. The reaction of cyanamide,NH₂CN(s) with dioxygen was carried out in a bomb calorimeter, and ∆U was found to be –742.7kJmol⁻¹ at 298 K. Calculate enthalpy change for the reaction at 298 K.

NH₂CN(g) + 3/2O₂(g)→N₂(g)+CO₂(g)+H₂O(l)

Solution :

Enthalpy change for a reaction (ΔH) is given by the expression,
ΔH = ΔU + Δn_gRT
Where,
ΔU = change in internal energy
Δn_g = change in number of moles
For the given reaction,
Δng = ∑n_g (products) – ∑n_g (reactants)
= (2 – 1.5) moles
Δn_g = 0.5 moles
And,
ΔU = –742.7 kJ mol^–1
T = 298 K
R = 8.314 × 10^–3 kJ mol^–1 K^–1
Substituting the values in the expression of ΔH:
ΔH = (–742.7 kJ mol^–1) + (0.5 mol) (298 K) (8.314 × 10^–3 kJ mol^–1 K^–1)
= –742.7 + 1.2
ΔH = –741.5 kJ mol^–1

9. Calculate the number of kJ of heat necessary to raise the temperature of 60.0 g of aluminium from 35°C to 55°C. Molar heat capacity of Al is 24 Jmol⁻¹K⁻¹.

Solution :

From the expression of heat (q) q=m⋅ c. ΔT 

Where, 

c= molar heat capacity 

m= mass of substance 

ΔT= change in temperature  

Substituting the values in the expression of q:

q=(60/27mol)(24Jmol⁻¹K⁻¹)(20K)

q=1066.7J

q=1.07k

10. Calculate the enthalpy change on freezing of 1.0 mol of water at10.0°C to ice at

–10.0°C.ΔfusH=6.03kJmol−1 at 0^∘C

C_p[H₂O(I)]=75.3Jmol₋₁K−1

C_ρ[H₂O(s)]=36.8Jmol⁻¹K⁻¹

Solution :

Total enthalpy change involved in the transformation is the of the following changes: 

(a) Energy change involved in the transformation of 1 mol of water at 10^∘ C to 1 mol of water at 0 C. 

(b) Energy change involved in the transformation of 1 mol of water at 0∘  to 1 mol of ice at 0^∘C

(c) Energy change involved in the transformation of 1 mol of ice at0∘C to 1 mol of ice at−10^∘C.

ΔH= C_p[ H₂OCl]ΔT+ ΔH _fivering + C_ρ[H₂O_(s)]ΔT

=(75.3] mol⁻¹K⁻¹)(0−10)K + (−6.03 × 10³Jmol⁻¹)+(36.8] mol⁻¹ K⁻¹ )(−10 −0)K

=−7533 mol⁻¹ − 6030Jmol ⁻¹− 368Jmol⁻¹

=−7151J mol⁻¹

=−7.151kJmol⁻¹

Hence, the enthalpy change involved in the transformation is−7.151kJmol⁻¹.

11. Enthalpy of combustion of carbon to CO₂ is –393.5−7.151kJmol⁻¹ . Calculate the heat released upon formation of 35.2 g ofCO₂  from carbon and dioxygen gas.

Solution :

Formation of CO₂  from carbon and dioxygen gas can be represented as: 

C(s) + O₂(g)⟶CO₂(g)

Δ_fH=−393.5kJmol⁻¹

(1 mole =44g) Heat released on formation of 44gCO₂=−393.5kJmol−1

∴ Heat released on formation of 35.2gCO₂

=−314.8kJmol⁻¹

12. Enthalpies of formation of CO(g), CO₂(g), N₂O(g) and N₂O₄(g) are −110,−393,81 and 9.7kJmol⁻¹ respectively.

Find the value of ∆H for the reaction: 

N₂O₄(g)+3CO(g)→N₂O(g+3CO₂(g]

Solution :

Δ_rH for a reaction is defined as the difference between ΔH value of products and ΔH value of reactants. 

Δ,H=∑Δ,H( products )−∑Δ_fH( reactants ) 

For the given reaction, 

N₂O_4(g) + 3CO_(g)⟶ N₂O_(g) + 3CO₂(g)

Δ_rH=[ {ΔfH(N₂O)+3ΔJH(CO₂)}−{ΔfH (N₂O₄) + 3ΔjH(CO)} ]

Substituting the values ofΔH for N₂O,CO₂,N₂O₄ , and CO

From the question, we get: 

Δ_rH=[ { 81kJmol⁻¹ + 3(−393)kJmol⁻¹} − {9.7kJmol ⁻¹+3(−110) kJmol⁻¹}]

Δ_rH=−7777kJmol⁻¹

Hence, the value ofΔ_rH

 for the reaction is −777.7 kJmol⁻¹.

13. Given

N₂(g) + 3H₂(g) ⟶ 2NH₃(y);

Δ_rHθ=−92.4kJmol⁻¹

What is the standard enthalpy of formation ofNH₃ gas?

Solution : Standard of formation of a compound is the charge in enthalpy that takes place during the formation of 1 mole Of a substance in its standard form from its constituent elements in their standard state. 

Re-writing the given equation for 1 mole of NH_3(g).

1/2N₂(g)+3/2H₂(g)⟶NH_3(g)

∴ Standard enthalpy of formation of NH_3(g)

=1/2 Δ_rHθ = 1/2(−92.4 kJmol⁻¹ )= −46.2kJmol⁻¹

14. Calculate the standard enthalpy of formation ofCH₃OH(l)  from the following data:

CH₃OH(l)+3/2O₂(g]→CO₂(g)+2H₂O(l): Δ,H∘=−726kJmol⁻¹

C(graphite) +O₂(g)→CO2(g]: ΔeH=−393kJmol⁻¹

H₂(g)+1/2O₂(g)→H₂O(1); Δ,H=−286kJmol⁻¹

Solution :

The reaction that takes place during the formation ofCH₃OH(l) can be written as:

C(s) + 2H₂O(g) + 1/2O₂(G), ⟶ CH₃OH(_η)(1)

The reaction (I) can be obtained from the given reactions by following the algebraic calculations as:

Equation (ii) + 2 × equation (iii) – equation (i)
Δ_fHθ [CH₃OH(l)] = ΔcH^θ + 2Δ_fH^θ [H₂O(l)] – Δ_rH^θ
= (–393 kJ mol^–1) + 2(–286 kJ mol^–1) – (–726 kJ mol^–1)
= (–393 – 572 + 726) kJ mol^–1
Δ_fH^θ [CH₃ OH(l)] = –239 kJ mol^–1

15. Calculate the enthalpy change for the process CCl₄(g)→C(g)+4Cl(g) and calculated bond enthalpy of C−Cl in CCl₄(g)

Δ_vapH^θ (CC|4) = 30.5kJmol⁻¹ Δ_fH^θ(CCl4) =−135.5kJmol−1

Δ_aH^θ(C) = 715.0kJmol⁻¹, where Δ_aH^θ  is enthalpy of atomisation 

Δ₂H^θ(Cl₂) = 242kJmol⁻¹

Solution :

 The chemical equations implying to the given values of enthalpies” are:
(1) CCl_4(l) à CCl_4(g) ; ΔvapH^Θ = 30.5 kJmol⁻¹
(2) C_(s) à C_(g) ΔaH^Θ = 715 kJmol⁻¹
(3) Cl2_(g) à 2Cl_(g) ; Δ_aH^Θ = 242 kJmol⁻¹
(4) C_(g) + 4Cl_(g) à CCl_4(g); ΔfH^Θ

= -135.5 kJmol⁻¹ ΔH for the process CCl_4(g) à C_(g) + 4Cl_(g) can be measured as:
ΔH=Δ_aH^Θ(C) + 2ΔaH^Θ(Cl₂) – Δ_vapH^Θ–ΔfH
= (715kJmol⁻¹) + 2(kJmol⁻¹) – (30.5kJmol⁻¹) – (-135.5kJmol⁻¹)
Therefore, H= 1304kJmol⁻¹
The value of bond enthalpy for C-Cl in CCl₄(g)
= 1304/4kJmol⁻¹
= 326 kJmol⁻¹

16. For an isolated system, ∆U = 0, what will be ∆S ?

Solution :
ΔS will be positive i.e., greater than zero
Since ΔU = 0, ΔS will be positive and the reaction will be spontaneous.

17. For the reaction at 298 K,

2A + B → C 

∆H = 400kJmol⁻¹

 and ∆S = 0.2kJmol⁻¹

At what temperature will the reaction become spontaneous considering ∆H and ∆S to be constant over the temperature range.

Solution :

From the expression

ΔG= ΔH−TΔS

Assuming the reaction at equilibrium,δ

 T for the reaction would be: 

T=(ΔH−ΔG)1/ΔS=ΔH/ΔS(ΔG=0 at equilibrium) 

=400kJmol⁻¹ 0.2 kJK⁻¹ mol⁻¹ T=2000K

For the reaction to be spontaneous,ΔG must be negative. Hence, for the given reaction to be spontaneous, T should be greater than 2000 K. 

18. For the reaction,2Cl(g)→Cl₂(g) , what are the signs of ∆H and ∆S ?

Solution :

∆H and ∆S are negative

The given reaction represents the formation of chlorine molecule from chlorine atoms. Here, bond formation is taking place. Therefore, energy Is being released. Hence ∆H is negative. 

Also, two moles of atoms have more randomness than one mole of a molecule. Since spontaneity is decreased, ∆S is negative for the given reaction. 

19. For the reaction

2A(g)+B(g)→2D(g)ΔUe=−10.5kJ and ΔS∘=−44.1JK⁻¹

Calculate ΔG^⊖ for the reaction, and predict whether the reaction may occur spontaneously

Solution :

For the given reaction,

2A(g)+B(g)→2D(g)Δηg=2−(3)=−1 mole 

Substituting the value of ΔU^θ

 in the expression of ΔH: 

ΔH^θ=ΔU^θ+Δn_gRT

=(−10.5kJ)−(−1)(8.314×10⁻³ kJK−1 mol⁻¹) (298K) = −10.5kJ⁻².48kJΔH^⊖=−12.98kJ

Substituting the values ofΔH^⊖ and ΔS^⊖ in the expression of ΔG^⊖

ΔG^θ= △H^θ−TΔS^θ

=−12.98kJ − ( 298K) (−44.1JK⁻¹) = −12.98kJ + 13.14 kJ ΔG^⊖ =+0.16kJ

SinceΔG^θ  for the reaction is positive, the reaction will not occur spontaneously. 

20. The equilibrium constant for a reaction is 10. What will be the value of ∆G^⊖ ? R = 8.314JK⁻¹ mol⁻¹

 T = 300 K.

Solution :

From the expression, ΔG^θ= −2.303 RT logk _eq

ΔG^θ for the reaction, 

=(2.303) (8.314JK⁻¹mol⁻¹) (300K) log10=−5744.14Jmol⁻¹

=−5.744kkmol⁻¹

21. Comment on the thermodynamic stability of NO(g) , given

12N_2(g)+12O_2(g)→NO_(g);

Δ_rH^⊖= 90kJmol⁻¹NO_(g) + 12O_2(g)→NO₂(g):

Δ_rH^e= −74kJmol⁻¹

Solution :

The positive value of Δ_rH indicates that heat is absorbed during the formation of NO(g), j. This means that NO(g) has higher than the reactants(N2 and O2) .

Hence, NO_(g) is unstable.  The negative value o_fΔ_rH

H indicates that heat is evolved during the formation ofNO_2(g) from NO_(g) and O_2(g)

. The product,NO_2(g)  is stabilized with minimum energy. 

Hence, unstableNO_(g) changes to unstableNO_2(g).

22. Calculate the entropy change in surroundings when 1.00 mol ofH₂O(l) is formed under standard conditions.ΔH^θ=−286kJ mol⁻¹

Solution :

It is given that 286 kJmol⁻¹ of heat is evolved the formation of 1 mol ofH₂O(l).

Thus, an equal amount of heat will be absorbed by the surroundings. 

q_surr= +286 kJmol⁻¹

Entropy change(ΔS_surr)  for the surroundings = q_surr / 7

=286kJmol⁻¹/ 298k

∴ΔS_surt =959.73 Jmol⁻¹K⁻¹