Chapter 3 : Chemical Kinetics
Chemistry
Answer the following Questions.
Question1. For the reaction R → P, the concentration of a reactant changes from 0.03 M to 0.02 M in 25 minutes. Calculate the average rate of reaction using units of time both in minutes and seconds.
Solution :
Average rate of reaction 

= 6.67 × 10−6 M s−1
Question2. In a reaction, 2A → Products, the concentration of A decreases from 0.5 mol L−1 to 0.4 mol L−1 in 10 minutes. Calculate the rate during this interval?
Solution :

= 0.005 mol L−1 min−1
= 5 × 10−3 M min−1
Question3. For a reaction, A + B → Product; the rate law is given by, r = k [A]½ [B]2. What is the order of the reaction?
Solution :
The order of the reaction r = k [A]½ [B]2
= 1 / 2 + 2
= 2.5
Question4. The conversion of molecules X to Y follows second order kinetics. If concentration of X is increased to three times how will it affect the rate of formation of Y?
Solution :
The reaction X → Y follows second order kinetics.
Therefore, the rate equation for this reaction will be:
Rate = k[X]2 (1)
Let [X] = a mol L−1, then equation (1) can be written as:
Rate1 = k .(a)2
= ka2
If the concentration of X is increased to three times, then [X] = 3a mol L−1
Now, the rate equation will be:
Rate = k (3a)2
= 9(ka2)
Hence, the rate of formation will increase by 9 times.
Question5. A first order reaction has a rate constant 1.15 10−3 s−1. How long will 5 g of this reactant take to reduce to 3 g?
Solution :
From the question, we can write down the following information:
Initial amount = 5 g
Final concentration = 3 g
Rate constant = 1.15 10−3 s−1
We know that for a 1st order reaction,

= 444.38 s
= 444 s (approx)
Question6. Time required to decompose SO2Cl2 to half of its initial amount is 60 minutes. If the decomposition is a first order reaction, calculate the rate constant of the reaction.
Solution :
We know that for a 1st order reaction,
t½ = 0.693 / k
It is given that t1/2 = 60 min
k = 0.693 / t½
= 0.693 / 60
= 0.01155 min-1
= 1.155 min-1
Or
k = 1.925 x 10-2 s-1
Question7. What will be the effect of temperature on rate constant?
Solution :
The rate constant of a reaction is nearly doubled with a 10° rise in temperature. However, the exact dependence of the rate of a chemical reaction on temperature is given by Arrhenius equation,
k = Ae – Ea / RT
Where,
A is the Arrhenius factor or the frequency factor
T is the temperature
R is the gas constant
Ea is the activation energy
Question8. The rate of the chemical reaction doubles for an increase of 10 K in absolute temperature from 298 K. Calculate Ea.
Solution :
It is given that T1 = 298 K
∴T2 = (298 + 10) K
= 308 K
We also know that the rate of the reaction doubles when temperature is increased by 10°.
Therefore, let us take the value of k1 = k and that of k2 = 2k
Also, R = 8.314 J K−1 mol−1
Now, substituting these values in the equation:

= 52897.78 J mol−1
= 52.9 kJ mol−1
Question9. The activation energy for the reaction 2HI(g) → H2 + I2(g) is 209.5 kJ mol−1 at 581K. Calculate the fraction of molecules of reactants having energy equal to or greater than activation energy?
Solution :
In the given case:
Ea = 209.5 kJ mol−1 = 209500 J mol−1
T = 581 K
R = 8.314 JK−1 mol−1
Now, the fraction of molecules of reactants having energy equal to or greater than activation energy is given as:
x = e−Ea / RT
⇒Inx= −Ea / RT
⇒logx=−Ea / 2.303RT
⇒logx= −209500Jmol−1 / 2.303 × 8.314JK−1mol−1×581
=−18.8323
Now,x= Antilog (−18.8323)
=1.471×10−19
Question10. From the rate expression for the following reactions, determine their order of reaction and the dimensions of the rate constants.
(i) 3 NO(g) → N2O (g) Rate = k[NO]2
(ii) H2O2 (aq) + 3 I− (aq) + 2 H+ → 2 H2O (l) + I3– Rate = k[H2O2][I−]
(iii) CH3CHO(g) → CH4(g) + CO(g) Rate = k [CH3CHO]3/2
(iv) C2H5Cl(g) → C2H4(g) + HCl(g) Rate = k [C2H5Cl]
Solution :
(i) Given rate = k [NO]2
Therefore, order of the reaction = 2
Dimension of k = Rate / [NO]2
= mol L-1 s-1 / (mol L-1)2
= mol L-1 s-1 / mol2 L-2
= L mol-1s-1
(ii) Given rate = k [H2O2] [I−]
Therefore, order of the reaction = 2
Dimension of
k = Rate / [H2O2][I – ]
= mol L-1 s-1 / (mol L-1) (mol L-1)
= L mol-1 s-1
(iii) Given rate = k [CH3CHO]3/2
Therefore, order of reaction = 3 / 2
Dimension of k = Rate / [CH3CHO]3/2
= mol L-1 s-1 / (mol L-1)3/2
= mol L-1 s-1 / mol3/2 L-3/2
= L½ mol-½ s-1
(iv) Given rate = k [C2H5Cl]
Therefore, order of the reaction = 1
Dimension of k = Rate / [C2H5Cl]
= mol L-1 s-1 / mol L-1
= s-1
Question11. For the reaction:
2A + B → A2B
the rate = k[A][B]2 with k = 2.0 × 10−6 mol−2 L2 s−1. Calculate the initial rate of the reaction when [A] = 0.1 mol L−1, [B] = 0.2 mol L−1. Calculate the rate of reaction after [A] is reduced to 0.06 mol L−1.
Solution :
The initial rate of the reaction is
Rate = k [A][B]2
= (2.0 × 10−6 mol−2 L2 s−1) (0.1 mol L−1) (0.2 mol L−1)2
= 8.0 × 10−9 mol−2 L2 s−1
When [A] is reduced from 0.1 mol L−1 to 0.06 mol−1, the concentration of A reacted = (0.1 − 0.06) mol L−1 = 0.04 mol L−1
Therefore, concentration of B reacted 1/2 x 0.04 mol L-1 = 0.02 mol L−1
Then, concentration of B available, [B] = (0.2 − 0.02) mol L−1
= 0.18 mol L−1
After [A] is reduced to 0.06 mol L−1, the rate of the reaction is given by,
Rate = k [A][B]2
= (2.0 × 10−6 mol−2 L2 s−1) (0.06 mol L−1) (0.18 mol L−1)2
= 3.89 mol L−1 s−1
Question12. The decomposition of NH3 on platinum surface is zero order reaction. What are the rates of production of N2 and H2 if k = 2.5 × 10−4 mol−1 L s−1?
Solution :
The decomposition of NH3 on platinum surface is represented by the following equation.

= 7.5 × 10−4 mol L−1 s−1
Question13. The decomposition of dimethyl ether leads to the formation of CH4, H2 and CO and the reaction rate is given by
Rate = k [CH3OCH3]3/2
The rate of reaction is followed by increase in pressure in a closed vessel, so the rate can also be expressed in terms of the partial pressure of dimethyl ether, i.e.,
rate = k (PCH3OCH3)3/2
If the pressure is measured in bar andtime in minutes, then what are the units of rate and rate constants?
Solution :
If pressure is measured in bar and time in minutes, then
Unit of rate = bar min−1
Rate = k [CH3OCH3]3/2
⇒ k =Rate / [CH3OCH3]3/2
Therefore, unit of rate constants(k) = bar min−1 / bar3/2
= bar-½ min -1
Question14. Mention the factors that affect the rate of a chemical reaction.
Solution :
The factors that affect the rate of a reaction are as follows.
(i) Concentration of reactants (pressure in case of gases)
(ii) Temperature
(iii) Presence of a catalyst
15. A reaction is second order with respect to a reactant. How is the rate of reaction affected if the concentration of the reactant is
(i) doubled (ii) reduced to half?
Solution :
Letthe concentration of the reactant be [A] = a
Rate of reaction, R = k [A]2
= ka2
(i)If the concentration of the reactant is doubled, i.e. [A] = 2a, then the rate of the reaction would be
R = k(2a)2
= 4ka2
= 4 R
Therefore, the rate of the reaction would increase by 4 times.
(ii) If the concentration of the reactant is reduced to half, i.e. [A] = 1/2 a , then the rate of the reaction would be
R = k(1/2a)2
= 1/4 Ka2
= 1/4 R
Therefore, the rate of the reaction would be reduced to
16. What change would happen in the rate constant of a reaction when there is a change in its temperature? How can this temperature effect on rate constant be represented quantitatively?
Solution :
When a temperature of 10∘ rises for a chemical reaction then the rate constant increases and becomes near to double of its original value.
The temperature effect on the rate constant can be represented quantitatively by Arrhenius equation,
k=Ae−Ea/RT
Where,
k = rate constant,
A = Frequency factor / Arrhenius factor,
R = gas constant
T = temperature
Ea = activation energy for the reaction.
Question17. In a pseudo first order hydrolysis of ester in water, the following results were obtained:
| t/s | 0 | 30 | 60 | 90 |
| [Ester]mol L−1 | 0.55 | 0.31 | 0.17 | 0.085 |
(i) Calculate the average rate of reaction between the time interval 30 to 60 seconds.
(ii) Calculate the pseudo first order rate constant for the hydrolysis of ester.
Solution :
(i) Average rate of reaction between the time interval, 30 to 60 seconds, d[ester] / dt
= (0.31-0.17) / (60-30)
= 0.14 / 30
= 4.67 × 10−3 mol L−1 s−1
(ii) For a pseudo first order reaction,
k = 2.303/ t log [R]º / [R]
For t = 30 s, k1
= 1.911 × 10−2 s−1
For t = 60 s, k1 = 2.303/ 30 log 0.55 / 0.31
= 1.957 × 10−2 s−1
For t = 90 s, k3 = 2.303/ 90 log 0.55 / 0.085
= 2.075 × 10 – 2s – 1
= 2.075 × 10−2 s−1
Then, average rate constant, k = k1 + k2+ k3 / 3
= 1.911 × 10 – 2 + 1.957 × 10 – 2 + 2.075 × 10 – 2 / 3
= 1.981 x 10-2 s – 1
Question18. A reaction is first order in A and second order in B.
(i) Write the differential rate equation.
(ii) How is the rate affected on increasing the concentration of B three times?
(iii) How is the rate affected when the concentrations of both A and B are doubled?
Solution :
(i) The differential rate equation will be

Question19. In a reaction between A and B, the initial rate of reaction (r0) was measured for different initial concentrations of A and B as given below:
| A/ mol L−1 | 0.20 | 0.20 | 0.40 |
| B/ mol L−1 | 0.30 | 0.10 | 0.05 |
| r0/ mol L−1 s−1 | 5.07 × 10−5 | 5.07 × 10−5 | 1.43 × 10−4 |
What is the order of the reaction with respect to A and B?
Solution :
Let the order of the reaction with respect to A be x and with respect to B be y.
Therefore,

Dividing equation (iii) by (ii), we obtain
= 1.496
= 1.5 (approximately)
Hence, the order of the reaction with respect to A is 1.5 and with respect to B is zero.
Question20. The following results have been obtained during the kinetic studies of the reaction:
2A + B → C + D
| Experiment | A/ mol L−1 | B/ mol L−1 | Initial rate of formation of D/mol L−1 min−1 |
| I | 0.1 | 0.1 | 6.0 × 10−3 |
| II | 0.3 | 0.2 | 7.2 × 10−2 |
| III | 0.3 | 0.4 | 2.88 × 10−1 |
| IV | 0.4 | 0.1 | 2.40 × 10−2 |
Determine the rate law and the rate constant for the reaction.
Solution :
Let the order of the reaction with respect to A be x and with respect to B be y.
Therefore, rate of the reaction is given by,

Dividing equation (iv) by (i), we obtain

Dividing equation (iii) by (ii), we obtain


Question21. The reaction between A and B is first order with respect to A and zero order with respect to B. Fill in the blanks in the following table:
| Experiment | A/ mol L−1 | B/ mol L−1 | Initial rate/mol L−1 min−1 |
| I | 0.1 | 0.1 | 2.0 × 10−2 |
| II | — | 0.2 | 4.0 × 10−2 |
| III | 0.4 | 0.4 | — |
| IV | — | 0.2 | 2.0 × 10−2 |
Solution :
The given reaction is of the first order with respect to A and of zero order with respect to B.
Therefore, the rate of the reaction is given by,
Rate = k [A]1 [B]0
⇒ Rate = k [A]
From experiment I, we obtain
2.0 × 10−2 mol L−1 min−1 = k (0.1 mol L−1)
⇒ k = 0.2 min−1
From experiment II, we obtain
4.0 × 10−2 mol L−1 min−1 = 0.2 min−1 [A]
⇒ [A] = 0.2 mol L−1
From experiment III, we obtain
Rate = 0.2 min−1 × 0.4 mol L−1
= 0.08 mol L−1 min−1
From experiment IV, we obtain
2.0 × 10−2 mol L−1 min−1 = 0.2 min−1 [A]
⇒ [A] = 0.1 mol L−1
Question22. Calculate the half-life of a first order reaction from their rate constants given below:
(i) 200 s−1 (ii) 2 min−1 (iii) 4 years−1
Solution :
(i) Half life, t 1/2 = 0.693 / k
= 0.693 / 200 s-1
= 3.47×10 -3 s (approximately)
(ii) Half life, t 1/2 = 0.693 / k
= 0.693 / 2 min-1
= 0.35 min (approximately)
(iii) Half life, t 1/2 = 0.693 / k
= 0.693 / 4 years-1
= 0.173 years (approximately)
Question23. The half-life for radioactive decay of 14C is 5730 years. An archaeological artifact containing wood had only 80% of the 14C found in a living tree. Estimate the age of the sample.
Solution :
Here, k = 0.693 / t1/2
= 0.693 / 5730 years-1
It is known that,

= 1845 years (approximately)
Hence, the age of the sample is 1845 years.
Question24. The experimental data for decomposition of N2O5
[2N2O5 → 4NO2 + O2] in gas phase at 318K are given below:
| t(s) | 0 | 400 | 800 | 1200 | 1600 | 2000 | 2400 | 2800 | 3200 |
| 102 × [N2O5] mol L-1 | 1.63 | 1.36 | 1.14 | 0.93 | 0.78 | 0.64 | 0.53 | 0.43 | 0.35 |
(i) Plot [N2O5] against t.
(ii) Find the half-life period for the reaction.
(iii) Draw a graph between log [N2O5] and t.
(iv) What is the rate law?
(v) Calculate the rate constant.
(vi) Calculate the half-life period from k and compare it with (ii).
Solution :
(ii) Time corresponding to the concentration, 1630×102 / 2 mol L-1 = 81.5 mol L-1 is the half life. From the graph, the half life is obtained as 1450 s.
(iii)
| t(s) | 102 × [N2O5] mol L-1 | Log[N2O5] |
| 0 | 1.63 | − 1.79 |
| 400 | 1.36 | − 1.87 |
| 800 | 1.14 | − 1.94 |
| 1200 | 0.93 | − 2.03 |
| 1600 | 0.78 | − 2.11 |
| 2000 | 0.64 | − 2.19 |
| 2400 | 0.53 | − 2.28 |
| 2800 | 0.43 | − 2.37 |
| 3200 | 0.35 | − 2.46 |

(iv) The given reaction is of the first order as the plot, Log[N2O5] v/s t, is a straight line. Therefore, the rate law of the reaction is
Rate = k [N2O5]
(v) From the plot, Log[N2O5] v/s t, we obtain
– k /2.303
Again, slope of the line of the plot Log[N2O5] v/s t is given by
– k / 2.303. = -0.67 / 3200
Therefore, we obtain,
– k / 2.303 = – 0.67 / 3200
⇒ k = 4.82 x 10-4 s-1
(vi) Half-life is given by,
t½ = 0.693 / k
= 0.639 / 4.82×10-4 s
=1.438 x 103
This value, 1438 s, is very close to the value that was obtained from the graph.
25. The rate constant for a first order reaction is 60 s−1. How much time will it take to reduce the initial concentration of the reactant to its 1/16th value?
Solution :
It is known that,

Question26. During nuclear explosion, one of the products is 90Sr with half-life of 28.1 years. If 1μg of 90Sr was absorbed in the bones of a newly born baby instead of calcium, how much of it will remain after 10 years and 60 years if it is not lost metabolically.
Solution :
,

Therefore, 0.7814 μg of 90Sr will remain after 10 years.
Again,

Therefore, 0.2278 μg of 90Sr will remain after 60 years.
Question27. For a first order reaction, show that time required for 99% completion is twice the time required for the completion of 90% of reaction.
Solution :
For a first order reaction, the time required for 99% completion is
t1 = 2.303/k Log 100/100-99
= 2.303/k Log 100
= 2x 2.303/k
For a first order reaction, the time required for 90% completion is
t2 = 2.303/k Log 100 / 100-90
= 2.303/k Log 10
= 2.303/k
Therefore, t1 = 2t2
Hence, the time required for 99% completion of a first order reaction is twice the time required for the completion of 90% of the reaction.
Question28. A first order reaction takes 40 min for 30% decomposition. Calculate t1/2.
Solution :
For a first order reaction,
t = 2.303/k Log [R] º / [R]
k = 2.303/40min Log 100 / 100-30
= 2.303/40min Log 10 / 7
= 8.918 x 10-3 min-1
Therefore, t1/2 of the decomposition reaction is
t1/2 = 0.693/k
= 0.693 / 8.918 x 10-3 min
= 77.7 min (approximately)
= 77.7 min (approximately)
Question29. For the decomposition of azoisopropane to hexane and nitrogen at 543 K, the following data are obtained.
| t (sec) | P(mm of Hg) |
| 0 | 35.0 |
| 360 | 54.0 |
| 720 | 63.0 |
Calculate the rate constant.
Solution :
The decomposition of azoisopropane to hexane and nitrogen at 543 K is represented by the following equation.
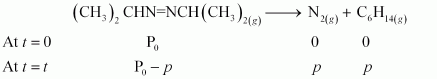
After time, t, total pressure, Pt = (Pº – p) + p + p
⇒ Pt = (Pº + p)
⇒ p = Pt – P0
therefore, Pº – p = P0 – Pt – P0
= 2P0 − Pt
For a first order reaction,
k = 2.303/t Log P0 /P0 – p
= 2.303/t Log P0 / 2 P0 – Pt
When t = 360 s, k = 2.303 / 360s log 35.0 / 2×35.0 – 54.0
= 2.175 × 10−3 s−1
When t = 720 s, k = 2.303 / 720s log 35.0 / 2×35.0 – 63.0
= 2.235 × 10−3 s−1
Hence, the average value of rate constant is
k = (2.175 × 10 – 3 + 2.235 × 10 – 3 ) / 2 s – 1
= 2.21 × 10−3 s−1
Question30. The following data were obtained during the first order thermal decomposition of SO2Cl2 at a constant volume.
SO2Cl2(g) → SO2(g) + Cl2(g)
| Experiment | Time/s−1 | Total pressure/atm |
| 1 | 0 | 0.5 |
| 2 | 100 | 0.6 |
Calculate the rate of the reaction when total pressure is 0.65 atm.
Solution :
The thermal decomposition of SO2Cl2 at a constant volume is represented by the following equation.

After time, t, total pressure, Pt = (Pº – p) + p + p
⇒ Pt = (Pº + p)
⇒ p = Pt – Pº
therefore, Pº – p = Pº – Pt – Pº
= 2 Pº – Pt
For a first order reaction,
k = 2.303/t Log Pº / Pº – p
= 2.303/t Log Pº / 2 Pº – Pt
When t= 100 s,
k = 2.303 / 100s log 0.5 / 2×0.5 – 0.6
= 2.231 × 10 – 3s – 1
When Pt= 0.65 atm,
P0+ p= 0.65
⇒ p= 0.65 – P0
= 0.65 – 0.5
= 0.15 atm
Therefore, when the total pressure is 0.65 atm, pressure of SOCl2 is
PSOCL2 = P0 – p
= 0.5 – 0.15
= 0.35 atm
Therefore, the rate of equation, when total pressure is 0.65 atm, is given by,
Rate = k(pSOCL2)
= (2.23 × 10 – 3s – 1) (0.35 atm)
= 7.8 × 10 – 4 atm s – 1
Question31. The rate constant for the decomposition of N2O5 at various temperatures is given below:
| T/°C | 0 | 20 | 40 | 60 | 80 |
| 105 X K /S-1 | 0.0787 | 1.70 | 25.7 | 178 | 2140 |
Draw a graph between ln k and 1/T and calculate the values of A and Ea.
Predict the rate constant at 30º and 50ºC.
Solution :
From the given data, we obtain
| T/°C | 0 | 20 | 40 | 60 | 80 |
| T/K | 273 | 293 | 313 | 333 | 353 |
| 1/T / k-1 | 3.66×10−3 | 3.41×10−3 | 3.19×10−3 | 3.0×10−3 | 2.83 ×10−3 |
| 105 X K /S-1 | 0.0787 | 1.70 | 25.7 | 178 | 2140 |
| ln k | −7.147 | − 4.075 | −1.359 | −0.577 | 3.063 |

Slope of the line,

In k= – 2.8
Therefore, k = 6.08×10-2s-1
Again when T = 50 + 273K = 323K,
1/T = 3.1 x 10-3 K
In k = – 0.5
Therefore, k = 0.607 s-1
Question32. The rate constant for the decomposition of hydrocarbons is 2.418 × 10−5 s−1 at 546 K. If the energy of activation is 179.9 kJ/mol, what will be the value of pre-exponential factor.
Solution :
k = 2.418 × 10−5 s−1
T = 546 K
Ea = 179.9 kJ mol−1 = 179.9 × 103 J mol−1
According to the Arrhenius equation,

= (0.3835 − 5) + 17.2082
= 12.5917
Therefore, A = antilog (12.5917)
= 3.9 × 1012 s−1 (approximately)
Question33. Consider a certain reaction A → Products with k = 2.0 × 10−2 s−1. Calculate the concentration of A remaining after 100 s if the initial concentration of A is 1.0 mol L−1.
Solution :
k = 2.0 × 10−2 s−1
T = 100 s
[A]o = 1.0 moL−1
Since the unit of k is s−1, the given reaction is a first order reaction.
Therefore, k = 2.303/t Log [A]º / [A]
⇒2.0 × 110-2 s-1 = 2.303/100s Log 1.0 / [A]
⇒2.0 × 110-2 s-1 = 2.303/100s ( – Log [A] )
⇒ – Log [A] = – (2.0 x 10-2 x 100) / 2.303
⇒ [A] = antilog [- (2.0 x 10-2 x 100) / 2.303]
= 0.135 mol L−1 (approximately)
Hence, the remaining concentration of A is 0.135 mol L−1.
Question34. Sucrose decomposes in acid solution into glucose and fructose according to the first order rate law, with t1/2 = 3.00 hours. What fraction of sample of sucrose remains after 8 hours?
Solution :For a first order reaction,
k = 2.303/t Log [R]º / [R]
It is given that, t1/2 = 3.00 hours
Therefore, k = 0.693 / t1/2
= 0.693 / 3 h-1
= 0.231 h – 1
Then, 0.231 h – 1 = 2.303 / 8h Log [R]º / [R]

Hence, the fraction of sample of sucrose that remains after 8 hours is 0.158.
Question35. The decomposition of hydrocarbon follows the equation k = (4.5 × 1011 s−1) e−28000 K/T Calculate Ea.
Solution :
The given equation is
k = (4.5 × 1011 s−1) e−28000 K/T (i)
Arrhenius equation is given by,
k= Ae -Ea/RT (ii)
From equation (i) and (ii), we obtain
Ea / RT = 28000K / T
⇒ Ea = R x 28000K
= 8.314 J K−1 mol−1 × 28000 K
= 232792 J mol−1
= 232.792 kJ mol−1
Question36. The rate constant for the first order decomposition of H2O2 is given by the following equation:
log k = 14.34 − 1.25 × 104 K/T
Calculate Ea for this reaction and at what temperature will its half-period be 256 minutes?
Solution :
Arrhenius equation is given by,
k= Ae -Ea/RT
⇒In k = In A – Ea/RT
⇒In k = Log A – Ea/RT
⇒ Log k = Log A – Ea/2.303RT (i)
The given equation is
Log k = 14.34 – 1.25 104 K/T (ii)
From equation (i) and (ii), we obtain
Ea/2.303RT = 1.25 104 K/T
= 1.25 × 104 K × 2.303 × 8.314 J K−1 mol−1
= 239339.3 J mol−1 (approximately)
= 239.34 kJ mol−1
Also, when t1/2 = 256 minutes,
k = 0.693 / t1/2
= 0.693 / 256
= 2.707 × 10 – 3 min – 1
= 4.51 × 10 – 5s – 1
= 2.707 × 10−3 min−1
= 4.51 × 10−5 s−1
It is also given that, log k = 14.34 − 1.25 × 104 K/T

= 668.95 K
= 669 K (approximately)
Question37. The decomposition of A into product has value of k as 4.5 × 103 s−1 at 10°C and energy of activation 60 kJ mol−1. At what temperature would k be 1.5 × 104 s−1?
Solution :
From Arrhenius equation, we obtain
log k2/k1 = Ea / 2.303 R (T2 – T1) / T1T2
Also, k1 = 4.5 × 103 s−1
T1 = 273 + 10 = 283 K
k2 = 1.5 × 104 s−1
Ea = 60 kJ mol−1 = 6.0 × 104 J mol−1
Then,

= 297 K
= 24°C
Hence, k would be 1.5 × 104 s−1 at 24°C.
Question38. The time required for 10% completion of a first order reaction at 298 K is equal to that required for its 25% completion at 308 K. If the value of A is 4 × 1010 s−1. Calculate k at 318 K and Ea.
Solution :
For a first order reaction,
t = 2.303 / k log a / a – x
At 298 K, t = 2.303 / k log 100 / 90
= 0.1054 / k
At 308 K, t’ = 2.303 / k’ log 100 / 75
= 2.2877 / k’
According to the question,
t = t’
⇒ 0.1054 / k = 2.2877 / k’
⇒ k’ / k = 2.7296
From Arrhenius equation, we obtain

To calculate k at 318 K,
It is given that, A = 4 x 1010 s-1, T = 318K
Again, from Arrhenius equation, we obtain

Therefore, k = Antilog (-1.9855)
= 1.034 x 10-2 s -1
Question39. The rate of a reaction quadruples when the temperature changes from 293 K to 313 K. Calculate the energy of activation of the reaction assuming that it does not change with temperature.
Solution :
From Arrhenius equation, we obtain

Hence, the required energy of activation is 52.86 kJmol−1.
NCERT Solutions For Class 12 Chemistry Chapter Wise.
- Chapter-1 The Solid States
- Chapter-2 Solutions
- Chapter-3 Electrochemistry
- Chapter-4 Chemical Kinetics
- Chapter-5 Surface Chemistry
- Chapter-6 General Priciples and Processes of Isolation of Elements
- Chapter-7 The P Block Elements
- Chapter-8 The D and F Elements
- Chapter-9 Coordination Compounds
- Chapter-10 Haloalkanes and Haloarenes
- Chapter-11 Alcohols, Phenols and Ethers
- Chapter-12 Aldehydes, ketones and Carboxylics Acids
- Chapter-13 Amines
- Chapter-14 Biomolecules
- Chapter-15 Polymers
- Chapter-16 Chemistry In Everyday Life
Question4. The conversion of molecules X to Y follows second order kinetics. If concentration of X is increased to three times how will it affect the rate of formation of Y?
Solution :
The reaction X → Y follows second order kinetics.
Therefore, the rate equation for this reaction will be:
Rate = k[X]2 (1)
Let [X] = a mol L−1, then equation (1) can be written as:
Rate1 = k .(a)2
= ka2
If the concentration of X is increased to three times, then [X] = 3a mol L−1
Now, the rate equation will be:
Rate = k (3a)2
= 9(ka2)
Hence, the rate of formation will increase by 9 times.
Question5. A first order reaction has a rate constant 1.15 10−3 s−1. How long will 5 g of this reactant take to reduce to 3 g?
Solution :
From the question, we can write down the following information:
Initial amount = 5 g
Final concentration = 3 g
Rate constant = 1.15 10−3 s−1
We know that for a 1st order reaction,

= 444.38 s
= 444 s (approx)
Question6. Time required to decompose SO2Cl2 to half of its initial amount is 60 minutes. If the decomposition is a first order reaction, calculate the rate constant of the reaction.
Solution :
We know that for a 1st order reaction,
t½ = 0.693 / k
It is given that t1/2 = 60 min
k = 0.693 / t½
= 0.693 / 60
= 0.01155 min-1
= 1.155 min-1
Or
k = 1.925 x 10-2 s-1
Question7. What will be the effect of temperature on rate constant?
Solution :
The rate constant of a reaction is nearly doubled with a 10° rise in temperature. However, the exact dependence of the rate of a chemical reaction on temperature is given by Arrhenius equation,
k = Ae – Ea / RT
Where,
A is the Arrhenius factor or the frequency factor
T is the temperature
R is the gas constant
Ea is the activation energy
Question8. The rate of the chemical reaction doubles for an increase of 10 K in absolute temperature from 298 K. Calculate Ea.
Solution :
It is given that T1 = 298 K
∴T2 = (298 + 10) K
= 308 K
We also know that the rate of the reaction doubles when temperature is increased by 10°.
Therefore, let us take the value of k1 = k and that of k2 = 2k
Also, R = 8.314 J K−1 mol−1
Now, substituting these values in the equation:

= 52897.78 J mol−1
= 52.9 kJ mol−1
Question9. The activation energy for the reaction 2HI(g) → H2 + I2(g) is 209.5 kJ mol−1 at 581K. Calculate the fraction of molecules of reactants having energy equal to or greater than activation energy?
Solution :
In the given case:
Ea = 209.5 kJ mol−1 = 209500 J mol−1
T = 581 K
R = 8.314 JK−1 mol−1
Now, the fraction of molecules of reactants having energy equal to or greater than activation energy is given as:
x = e−Ea / RT
⇒Inx= −Ea / RT
⇒logx=−Ea / 2.303RT
⇒logx= −209500Jmol−1 / 2.303 × 8.314JK−1mol−1×581
=−18.8323
Now,x= Antilog (−18.8323)
=1.471×10−19
Question10. From the rate expression for the following reactions, determine their order of reaction and the dimensions of the rate constants.
(i) 3 NO(g) → N2O (g) Rate = k[NO]2
(ii) H2O2 (aq) + 3 I− (aq) + 2 H+ → 2 H2O (l) + I3– Rate = k[H2O2][I−]
(iii) CH3CHO(g) → CH4(g) + CO(g) Rate = k [CH3CHO]3/2
(iv) C2H5Cl(g) → C2H4(g) + HCl(g) Rate = k [C2H5Cl]
Solution :
(i) Given rate = k [NO]2
Therefore, order of the reaction = 2
Dimension of k = Rate / [NO]2
= mol L-1 s-1 / (mol L-1)2
= mol L-1 s-1 / mol2 L-2
= L mol-1s-1
(ii) Given rate = k [H2O2] [I−]
Therefore, order of the reaction = 2
Dimension of
k = Rate / [H2O2][I – ]
= mol L-1 s-1 / (mol L-1) (mol L-1)
= L mol-1 s-1
(iii) Given rate = k [CH3CHO]3/2
Therefore, order of reaction = 3 / 2
Dimension of k = Rate / [CH3CHO]3/2
= mol L-1 s-1 / (mol L-1)3/2
= mol L-1 s-1 / mol3/2 L-3/2
= L½ mol-½ s-1
(iv) Given rate = k [C2H5Cl]
Therefore, order of the reaction = 1
Dimension of k = Rate / [C2H5Cl]
= mol L-1 s-1 / mol L-1
= s-1
Question11. For the reaction:
2A + B → A2B
the rate = k[A][B]2 with k = 2.0 × 10−6 mol−2 L2 s−1. Calculate the initial rate of the reaction when [A] = 0.1 mol L−1, [B] = 0.2 mol L−1. Calculate the rate of reaction after [A] is reduced to 0.06 mol L−1.
Solution :
The initial rate of the reaction is
Rate = k [A][B]2
= (2.0 × 10−6 mol−2 L2 s−1) (0.1 mol L−1) (0.2 mol L−1)2
= 8.0 × 10−9 mol−2 L2 s−1
When [A] is reduced from 0.1 mol L−1 to 0.06 mol−1, the concentration of A reacted = (0.1 − 0.06) mol L−1 = 0.04 mol L−1
Therefore, concentration of B reacted 1/2 x 0.04 mol L-1 = 0.02 mol L−1
Then, concentration of B available, [B] = (0.2 − 0.02) mol L−1
= 0.18 mol L−1
After [A] is reduced to 0.06 mol L−1, the rate of the reaction is given by,
Rate = k [A][B]2
= (2.0 × 10−6 mol−2 L2 s−1) (0.06 mol L−1) (0.18 mol L−1)2
= 3.89 mol L−1 s−1
Question12. The decomposition of NH3 on platinum surface is zero order reaction. What are the rates of production of N2 and H2 if k = 2.5 × 10−4 mol−1 L s−1?
Solution :
The decomposition of NH3 on platinum surface is represented by the following equation.

= 7.5 × 10−4 mol L−1 s−1
Question13. The decomposition of dimethyl ether leads to the formation of CH4, H2 and CO and the reaction rate is given by
Rate = k [CH3OCH3]3/2
The rate of reaction is followed by increase in pressure in a closed vessel, so the rate can also be expressed in terms of the partial pressure of dimethyl ether, i.e.,
rate = k (PCH3OCH3)3/2
If the pressure is measured in bar andtime in minutes, then what are the units of rate and rate constants?
Solution :
If pressure is measured in bar and time in minutes, then
Unit of rate = bar min−1
Rate = k [CH3OCH3]3/2
⇒ k =Rate / [CH3OCH3]3/2
Therefore, unit of rate constants(k) = bar min−1 / bar3/2
= bar-½ min -1
Question14. Mention the factors that affect the rate of a chemical reaction.
Solution :
The factors that affect the rate of a reaction are as follows.
(i) Concentration of reactants (pressure in case of gases)
(ii) Temperature
(iii) Presence of a catalyst
15. A reaction is second order with respect to a reactant. How is the rate of reaction affected if the concentration of the reactant is
(i) doubled (ii) reduced to half?
Solution :
Letthe concentration of the reactant be [A] = a
Rate of reaction, R = k [A]2
= ka2
(i)If the concentration of the reactant is doubled, i.e. [A] = 2a, then the rate of the reaction would be
R = k(2a)2
= 4ka2
= 4 R
Therefore, the rate of the reaction would increase by 4 times.
(ii) If the concentration of the reactant is reduced to half, i.e. [A] = 1/2 a , then the rate of the reaction would be
R = k(1/2a)2
= 1/4 Ka2
= 1/4 R
Therefore, the rate of the reaction would be reduced to
16. What change would happen in the rate constant of a reaction when there is a change in its temperature? How can this temperature effect on rate constant be represented quantitatively?
Solution :
When a temperature of 10∘ rises for a chemical reaction then the rate constant increases and becomes near to double of its original value.
The temperature effect on the rate constant can be represented quantitatively by Arrhenius equation,
k=Ae−Ea/RT
Where,
k = rate constant,
A = Frequency factor / Arrhenius factor,
R = gas constant
T = temperature
Ea = activation energy for the reaction.
Question17. In a pseudo first order hydrolysis of ester in water, the following results were obtained:
| t/s | 0 | 30 | 60 | 90 |
| [Ester]mol L−1 | 0.55 | 0.31 | 0.17 | 0.085 |
(i) Calculate the average rate of reaction between the time interval 30 to 60 seconds.
(ii) Calculate the pseudo first order rate constant for the hydrolysis of ester.
Solution :
(i) Average rate of reaction between the time interval, 30 to 60 seconds, d[ester] / dt
= (0.31-0.17) / (60-30)
= 0.14 / 30
= 4.67 × 10−3 mol L−1 s−1
(ii) For a pseudo first order reaction,
k = 2.303/ t log [R]º / [R]
For t = 30 s, k1
= 1.911 × 10−2 s−1
For t = 60 s, k1 = 2.303/ 30 log 0.55 / 0.31
= 1.957 × 10−2 s−1
For t = 90 s, k3 = 2.303/ 90 log 0.55 / 0.085
= 2.075 × 10 – 2s – 1
= 2.075 × 10−2 s−1
Then, average rate constant, k = k1 + k2+ k3 / 3
= 1.911 × 10 – 2 + 1.957 × 10 – 2 + 2.075 × 10 – 2 / 3
= 1.981 x 10-2 s – 1
Question18. A reaction is first order in A and second order in B.
(i) Write the differential rate equation.
(ii) How is the rate affected on increasing the concentration of B three times?
(iii) How is the rate affected when the concentrations of both A and B are doubled?
Solution :
(i) The differential rate equation will be

Question19. In a reaction between A and B, the initial rate of reaction (r0) was measured for different initial concentrations of A and B as given below:
| A/ mol L−1 | 0.20 | 0.20 | 0.40 |
| B/ mol L−1 | 0.30 | 0.10 | 0.05 |
| r0/ mol L−1 s−1 | 5.07 × 10−5 | 5.07 × 10−5 | 1.43 × 10−4 |
What is the order of the reaction with respect to A and B?
Solution :
Let the order of the reaction with respect to A be x and with respect to B be y.
Therefore,

Dividing equation (iii) by (ii), we obtain
= 1.496
= 1.5 (approximately)
Hence, the order of the reaction with respect to A is 1.5 and with respect to B is zero.
Question20. The following results have been obtained during the kinetic studies of the reaction:
2A + B → C + D
| Experiment | A/ mol L−1 | B/ mol L−1 | Initial rate of formation of D/mol L−1 min−1 |
| I | 0.1 | 0.1 | 6.0 × 10−3 |
| II | 0.3 | 0.2 | 7.2 × 10−2 |
| III | 0.3 | 0.4 | 2.88 × 10−1 |
| IV | 0.4 | 0.1 | 2.40 × 10−2 |
Determine the rate law and the rate constant for the reaction.
Solution :
Let the order of the reaction with respect to A be x and with respect to B be y.
Therefore, rate of the reaction is given by,

Dividing equation (iv) by (i), we obtain

Dividing equation (iii) by (ii), we obtain


Question21. The reaction between A and B is first order with respect to A and zero order with respect to B. Fill in the blanks in the following table:
| Experiment | A/ mol L−1 | B/ mol L−1 | Initial rate/mol L−1 min−1 |
| I | 0.1 | 0.1 | 2.0 × 10−2 |
| II | — | 0.2 | 4.0 × 10−2 |
| III | 0.4 | 0.4 | — |
| IV | — | 0.2 | 2.0 × 10−2 |
Solution :
The given reaction is of the first order with respect to A and of zero order with respect to B.
Therefore, the rate of the reaction is given by,
Rate = k [A]1 [B]0
⇒ Rate = k [A]
From experiment I, we obtain
2.0 × 10−2 mol L−1 min−1 = k (0.1 mol L−1)
⇒ k = 0.2 min−1
From experiment II, we obtain
4.0 × 10−2 mol L−1 min−1 = 0.2 min−1 [A]
⇒ [A] = 0.2 mol L−1
From experiment III, we obtain
Rate = 0.2 min−1 × 0.4 mol L−1
= 0.08 mol L−1 min−1
From experiment IV, we obtain
2.0 × 10−2 mol L−1 min−1 = 0.2 min−1 [A]
⇒ [A] = 0.1 mol L−1
Question22. Calculate the half-life of a first order reaction from their rate constants given below:
(i) 200 s−1 (ii) 2 min−1 (iii) 4 years−1
Solution :
(i) Half life, t 1/2 = 0.693 / k
= 0.693 / 200 s-1
= 3.47×10 -3 s (approximately)
(ii) Half life, t 1/2 = 0.693 / k
= 0.693 / 2 min-1
= 0.35 min (approximately)
(iii) Half life, t 1/2 = 0.693 / k
= 0.693 / 4 years-1
= 0.173 years (approximately)
Question23. The half-life for radioactive decay of 14C is 5730 years. An archaeological artifact containing wood had only 80% of the 14C found in a living tree. Estimate the age of the sample.
Solution :
Here, k = 0.693 / t1/2
= 0.693 / 5730 years-1
It is known that,

= 1845 years (approximately)
Hence, the age of the sample is 1845 years.
Question24. The experimental data for decomposition of N2O5
[2N2O5 → 4NO2 + O2] in gas phase at 318K are given below:
| t(s) | 0 | 400 | 800 | 1200 | 1600 | 2000 | 2400 | 2800 | 3200 |
| 102 × [N2O5] mol L-1 | 1.63 | 1.36 | 1.14 | 0.93 | 0.78 | 0.64 | 0.53 | 0.43 | 0.35 |
(i) Plot [N2O5] against t.
(ii) Find the half-life period for the reaction.
(iii) Draw a graph between log [N2O5] and t.
(iv) What is the rate law?
(v) Calculate the rate constant.
(vi) Calculate the half-life period from k and compare it with (ii).
Solution :
(ii) Time corresponding to the concentration, 1630×102 / 2 mol L-1 = 81.5 mol L-1 is the half life. From the graph, the half life is obtained as 1450 s.
(iii)
| t(s) | 102 × [N2O5] mol L-1 | Log[N2O5] |
| 0 | 1.63 | − 1.79 |
| 400 | 1.36 | − 1.87 |
| 800 | 1.14 | − 1.94 |
| 1200 | 0.93 | − 2.03 |
| 1600 | 0.78 | − 2.11 |
| 2000 | 0.64 | − 2.19 |
| 2400 | 0.53 | − 2.28 |
| 2800 | 0.43 | − 2.37 |
| 3200 | 0.35 | − 2.46 |

(iv) The given reaction is of the first order as the plot, Log[N2O5] v/s t, is a straight line. Therefore, the rate law of the reaction is
Rate = k [N2O5]
(v) From the plot, Log[N2O5] v/s t, we obtain
– k /2.303
Again, slope of the line of the plot Log[N2O5] v/s t is given by
– k / 2.303. = -0.67 / 3200
Therefore, we obtain,
– k / 2.303 = – 0.67 / 3200
⇒ k = 4.82 x 10-4 s-1
(vi) Half-life is given by,
t½ = 0.693 / k
= 0.639 / 4.82×10-4 s
=1.438 x 103
This value, 1438 s, is very close to the value that was obtained from the graph.
25. The rate constant for a first order reaction is 60 s−1. How much time will it take to reduce the initial concentration of the reactant to its 1/16th value?
Solution :
It is known that,

Question26. During nuclear explosion, one of the products is 90Sr with half-life of 28.1 years. If 1μg of 90Sr was absorbed in the bones of a newly born baby instead of calcium, how much of it will remain after 10 years and 60 years if it is not lost metabolically.
Solution :
,

Therefore, 0.7814 μg of 90Sr will remain after 10 years.
Again,

Therefore, 0.2278 μg of 90Sr will remain after 60 years.
Question27. For a first order reaction, show that time required for 99% completion is twice the time required for the completion of 90% of reaction.
Solution :
For a first order reaction, the time required for 99% completion is
t1 = 2.303/k Log 100/100-99
= 2.303/k Log 100
= 2x 2.303/k
For a first order reaction, the time required for 90% completion is
t2 = 2.303/k Log 100 / 100-90
= 2.303/k Log 10
= 2.303/k
Therefore, t1 = 2t2
Hence, the time required for 99% completion of a first order reaction is twice the time required for the completion of 90% of the reaction.
Question28. A first order reaction takes 40 min for 30% decomposition. Calculate t1/2.
Solution :
For a first order reaction,
t = 2.303/k Log [R] º / [R]
k = 2.303/40min Log 100 / 100-30
= 2.303/40min Log 10 / 7
= 8.918 x 10-3 min-1
Therefore, t1/2 of the decomposition reaction is
t1/2 = 0.693/k
= 0.693 / 8.918 x 10-3 min
= 77.7 min (approximately)
= 77.7 min (approximately)
Question29. For the decomposition of azoisopropane to hexane and nitrogen at 543 K, the following data are obtained.
| t (sec) | P(mm of Hg) |
| 0 | 35.0 |
| 360 | 54.0 |
| 720 | 63.0 |
Calculate the rate constant.
Solution :
The decomposition of azoisopropane to hexane and nitrogen at 543 K is represented by the following equation.
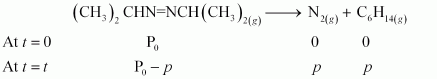
After time, t, total pressure, Pt = (Pº – p) + p + p
⇒ Pt = (Pº + p)
⇒ p = Pt – P0
therefore, Pº – p = P0 – Pt – P0
= 2P0 − Pt
For a first order reaction,
k = 2.303/t Log P0 /P0 – p
= 2.303/t Log P0 / 2 P0 – Pt
When t = 360 s, k = 2.303 / 360s log 35.0 / 2×35.0 – 54.0
= 2.175 × 10−3 s−1
When t = 720 s, k = 2.303 / 720s log 35.0 / 2×35.0 – 63.0
= 2.235 × 10−3 s−1
Hence, the average value of rate constant is
k = (2.175 × 10 – 3 + 2.235 × 10 – 3 ) / 2 s – 1
= 2.21 × 10−3 s−1
Question30. The following data were obtained during the first order thermal decomposition of SO2Cl2 at a constant volume.
SO2Cl2(g) → SO2(g) + Cl2(g)
| Experiment | Time/s−1 | Total pressure/atm |
| 1 | 0 | 0.5 |
| 2 | 100 | 0.6 |
Calculate the rate of the reaction when total pressure is 0.65 atm.
Solution :
The thermal decomposition of SO2Cl2 at a constant volume is represented by the following equation.

After time, t, total pressure, Pt = (Pº – p) + p + p
⇒ Pt = (Pº + p)
⇒ p = Pt – Pº
therefore, Pº – p = Pº – Pt – Pº
= 2 Pº – Pt
For a first order reaction,
k = 2.303/t Log Pº / Pº – p
= 2.303/t Log Pº / 2 Pº – Pt
When t= 100 s,
k = 2.303 / 100s log 0.5 / 2×0.5 – 0.6
= 2.231 × 10 – 3s – 1
When Pt= 0.65 atm,
P0+ p= 0.65
⇒ p= 0.65 – P0
= 0.65 – 0.5
= 0.15 atm
Therefore, when the total pressure is 0.65 atm, pressure of SOCl2 is
PSOCL2 = P0 – p
= 0.5 – 0.15
= 0.35 atm
Therefore, the rate of equation, when total pressure is 0.65 atm, is given by,
Rate = k(pSOCL2)
= (2.23 × 10 – 3s – 1) (0.35 atm)
= 7.8 × 10 – 4 atm s – 1
Question31. The rate constant for the decomposition of N2O5 at various temperatures is given below:
| T/°C | 0 | 20 | 40 | 60 | 80 |
| 105 X K /S-1 | 0.0787 | 1.70 | 25.7 | 178 | 2140 |
Draw a graph between ln k and 1/T and calculate the values of A and Ea.
Predict the rate constant at 30º and 50ºC.
Solution :
From the given data, we obtain
| T/°C | 0 | 20 | 40 | 60 | 80 |
| T/K | 273 | 293 | 313 | 333 | 353 |
| 1/T / k-1 | 3.66×10−3 | 3.41×10−3 | 3.19×10−3 | 3.0×10−3 | 2.83 ×10−3 |
| 105 X K /S-1 | 0.0787 | 1.70 | 25.7 | 178 | 2140 |
| ln k | −7.147 | − 4.075 | −1.359 | −0.577 | 3.063 |

Slope of the line,

In k= – 2.8
Therefore, k = 6.08×10-2s-1
Again when T = 50 + 273K = 323K,
1/T = 3.1 x 10-3 K
In k = – 0.5
Therefore, k = 0.607 s-1
Question32. The rate constant for the decomposition of hydrocarbons is 2.418 × 10−5 s−1 at 546 K. If the energy of activation is 179.9 kJ/mol, what will be the value of pre-exponential factor.
Solution :
k = 2.418 × 10−5 s−1
T = 546 K
Ea = 179.9 kJ mol−1 = 179.9 × 103 J mol−1
According to the Arrhenius equation,

= (0.3835 − 5) + 17.2082
= 12.5917
Therefore, A = antilog (12.5917)
= 3.9 × 1012 s−1 (approximately)
Question33. Consider a certain reaction A → Products with k = 2.0 × 10−2 s−1. Calculate the concentration of A remaining after 100 s if the initial concentration of A is 1.0 mol L−1.
Solution :
k = 2.0 × 10−2 s−1
T = 100 s
[A]o = 1.0 moL−1
Since the unit of k is s−1, the given reaction is a first order reaction.
Therefore, k = 2.303/t Log [A]º / [A]
⇒2.0 × 110-2 s-1 = 2.303/100s Log 1.0 / [A]
⇒2.0 × 110-2 s-1 = 2.303/100s ( – Log [A] )
⇒ – Log [A] = – (2.0 x 10-2 x 100) / 2.303
⇒ [A] = antilog [- (2.0 x 10-2 x 100) / 2.303]
= 0.135 mol L−1 (approximately)
Hence, the remaining concentration of A is 0.135 mol L−1.
Question34. Sucrose decomposes in acid solution into glucose and fructose according to the first order rate law, with t1/2 = 3.00 hours. What fraction of sample of sucrose remains after 8 hours?
Solution :For a first order reaction,
k = 2.303/t Log [R]º / [R]
It is given that, t1/2 = 3.00 hours
Therefore, k = 0.693 / t1/2
= 0.693 / 3 h-1
= 0.231 h – 1
Then, 0.231 h – 1 = 2.303 / 8h Log [R]º / [R]

Hence, the fraction of sample of sucrose that remains after 8 hours is 0.158.
Question35. The decomposition of hydrocarbon follows the equation k = (4.5 × 1011 s−1) e−28000 K/T Calculate Ea.
Solution :
The given equation is
k = (4.5 × 1011 s−1) e−28000 K/T (i)
Arrhenius equation is given by,
k= Ae -Ea/RT (ii)
From equation (i) and (ii), we obtain
Ea / RT = 28000K / T
⇒ Ea = R x 28000K
= 8.314 J K−1 mol−1 × 28000 K
= 232792 J mol−1
= 232.792 kJ mol−1
Question36. The rate constant for the first order decomposition of H2O2 is given by the following equation:
log k = 14.34 − 1.25 × 104 K/T
Calculate Ea for this reaction and at what temperature will its half-period be 256 minutes?
Solution :
Arrhenius equation is given by,
k= Ae -Ea/RT
⇒In k = In A – Ea/RT
⇒In k = Log A – Ea/RT
⇒ Log k = Log A – Ea/2.303RT (i)
The given equation is
Log k = 14.34 – 1.25 104 K/T (ii)
From equation (i) and (ii), we obtain
Ea/2.303RT = 1.25 104 K/T
= 1.25 × 104 K × 2.303 × 8.314 J K−1 mol−1
= 239339.3 J mol−1 (approximately)
= 239.34 kJ mol−1
Also, when t1/2 = 256 minutes,
k = 0.693 / t1/2
= 0.693 / 256
= 2.707 × 10 – 3 min – 1
= 4.51 × 10 – 5s – 1
= 2.707 × 10−3 min−1
= 4.51 × 10−5 s−1
It is also given that, log k = 14.34 − 1.25 × 104 K/T

= 668.95 K
= 669 K (approximately)
Question37. The decomposition of A into product has value of k as 4.5 × 103 s−1 at 10°C and energy of activation 60 kJ mol−1. At what temperature would k be 1.5 × 104 s−1?
Solution :
From Arrhenius equation, we obtain
log k2/k1 = Ea / 2.303 R (T2 – T1) / T1T2
Also, k1 = 4.5 × 103 s−1
T1 = 273 + 10 = 283 K
k2 = 1.5 × 104 s−1
Ea = 60 kJ mol−1 = 6.0 × 104 J mol−1
Then,

= 297 K
= 24°C
Hence, k would be 1.5 × 104 s−1 at 24°C.
Question38. The time required for 10% completion of a first order reaction at 298 K is equal to that required for its 25% completion at 308 K. If the value of A is 4 × 1010 s−1. Calculate k at 318 K and Ea.
Solution :
For a first order reaction,
t = 2.303 / k log a / a – x
At 298 K, t = 2.303 / k log 100 / 90
= 0.1054 / k
At 308 K, t’ = 2.303 / k’ log 100 / 75
= 2.2877 / k’
According to the question,
t = t’
⇒ 0.1054 / k = 2.2877 / k’
⇒ k’ / k = 2.7296
From Arrhenius equation, we obtain

To calculate k at 318 K,
It is given that, A = 4 x 1010 s-1, T = 318K
Again, from Arrhenius equation, we obtain

Therefore, k = Antilog (-1.9855)
= 1.034 x 10-2 s -1
Question39. The rate of a reaction quadruples when the temperature changes from 293 K to 313 K. Calculate the energy of activation of the reaction assuming that it does not change with temperature.
Solution :
From Arrhenius equation, we obtain

Hence, the required energy of activation is 52.86 kJmol−1.

